You asked for it so here it is, the follow up part 2 of the Physics of Sports. In case you missed part 1 of the physics of sport series, click HERE. Where we delved into the basic physical concepts of sport such as force, velocity and momentum and explored the practical application of the science.
 Work
Work
Work, in physics terms, occurs when a force is applied to an object and causes a displacement of that object.
W=F Δd
Where:
W=Work (J)
F=Force (N)
d=distance (m)
Work is done whenever a force causes displacement of an object. In strength training, generally we want to perform as much work as possible for a given exercise. An example of maximising work during an exercise would be squatting through a full range of motion, hips below the knees. This maximises the displacement of the barbell resulting in more work being done. We could also load a heavier barbell and only squat half of the range of motion to increase the work done. However, by increasing work this way we do not maximise leg muscle recruitment and also make ourselves more susceptible to injury.
Torque
Torque can be defined as a measure of the force required to rotate an object around a fixed axis. Below is a simple diagram describing how a torque is generated. From the equation and diagram there are two ways to create a larger torque, either by increasing the radius of where the force is applied to the body or by generating a larger force.
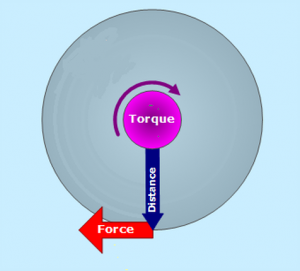
Torque Diagram
τ=Fr
Where:
τ=Torque (N.m)
F=Force (N)
r=radius (m)
A good example to demonstrate torque is the back extension exercise. The fixed axis being the hips against the pad. The upper body rotates around this fixed point. There are a couple of ways we can increase torque production, just by where we place our arms. The radius stems from the hip to the top of the head. If we put our arms straight overhead, we have now increased the radius by the length of our arms making the exercise more difficult and subsequently increasing torque production. To improve the force side of the equation, we can load the movement by holding a weight. Holding a weight at your chest will increase the force needed to perform the movement and therefore torque. The further the weight is placed from the point of rotation, the harder the exercise will be. E.g. weight overhead compared to weight held at chest.
Moment
A Moment is a very similar concept to a Torque, however without going into the fundamental physics and mathematics differentiating the two concepts, we will stick to the engineering distinction, between the two concepts. Where a Moment applies to a static objects and a Torque relating to dynamic objects rotating.
A Moment of a force is a measure of the forces tendency to cause a static object to rotate about a specific point. The force acts upon the object in a way that induces the object to begin twisting i.e. the force is applied to the object in a manner that the force does pass through the centroid (centre/midline) of the object.
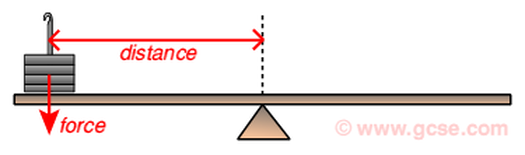
Moment Diagram
M=Fd
Where:
M=Moment (N.m)
F=Force (N)
d=distance (m)
Angular velocity
Angular Velocity is a vector quantity and is defined as the rate of change of angular displacement, that specifies the angular or rotational speed of an object about an axis of rotation.
What on earth does that actually mean? Basically this is the speed an object or body rotates around a point. This is a very similar concept to linear velocity.
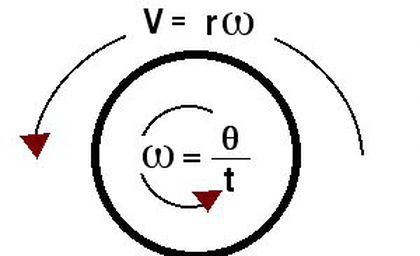
ω= θ/t
Where:
ω= Angular Velocity (rad/s)
θ=Angular Velocity (rad)
t=time (s)
Tangential Velocity of a point in Angular Velocity
V= ωr
Where:
V= Velocity (ms-1)
ω= Angular Velocity (rad/s)
r= radius (m)
Radius is generally fixed in sport e.g. tennis, golf and arm length. So angular velocity has to be improved in order to improve “overall” velocity. This can be done through strength and power exercises performed in the transverse plane (rotational). Some examples are various cable chops and rotary medicine ball throws.
Angular Momentum
Angular Momentum is a similar concept to linear momentum that we discussed in Part 1 of this series, however now we are introducing rotational motion to an object.
Angular Momentum of a rigid object can be defined as the product of the moment of inertia and the angular velocity.
L= Iω
Where:
L= Angular Momentum (kg.m2s-1)
ω= Angular Velocity (rad/s)
I= Moment of inertia (kg.m2)
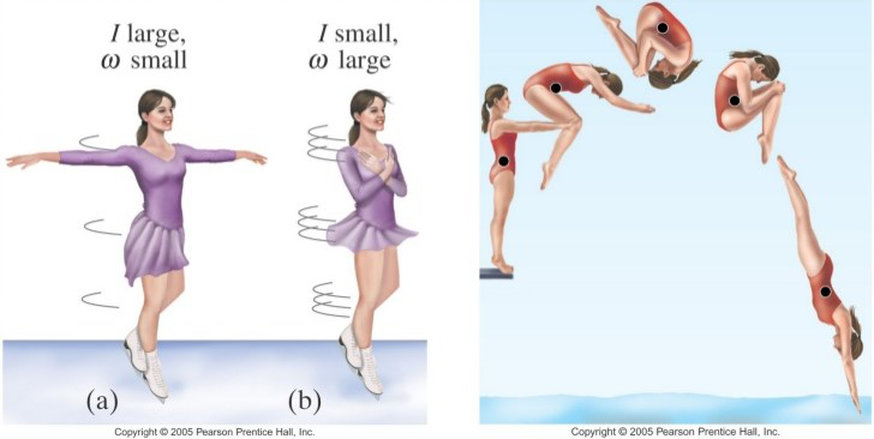
Conservation of Angular Momentum for an Ice Skater and a Diver
A good example of where angular momentum is applied to sport in the real world is with ice skaters, divers or gymnasts, when these athletes spin. Because of the laws of conservation, when the athlete starts the spinning movement they will have a specific angular momentum and this will stay constant until another force acts upon the athlete. If the athlete started their spin too slow and they can feel they won’t make the flip or finish the spin in the correct position, they will need to increase their angular velocity or face a rather nasty landing.
How can this athlete save themselves? The answer is reducing our moment of inertia, since angular momentum is constant. If the athlete forms a tighter tuck and brings their arms or legs closer to the centre of their body, they will instantaneously speed up their angular velocity.
Try This Yourself at Home:
If you have an office chair that spins, start by sitting in the chair with your arms out wide and get a partner to spin you. Once you are spinning, move your arms closer to the centre of your body. Can you feel the speed of your rotation speed up?
To really accentuate this, pick up a couple of 1-2kg weights or cans of food and place one in each hand and now get your partner to spin you and repeat the same process as above. This should dramatically increase your speed of rotation.
